Computer simulations are important tools for the area since they can explain numerous phenomena observed experimentally, as well as propose new phenomena and new experiments. Several research projects linked to the Graduate Program in Nanosciences and Advanced Materials focus on the study of materials from a computational point of view. UFABC has a large computational infrastructure to support these researchers and their students, including a dedicated data center with more than 3000 processors available for use. The works developed to cover several different themes, ranging from the study of crystalline materials, through two-dimensional (2D) materials and even the modeling of important complex biochemical processes that occur within human cells. Indeed, nanotechnology has applications that go beyond the boundaries of conventional materials.

Lipid nanoemulsions are promising nanomaterials for drug delivery applications in food, pharmaceutical and cosmetic industries. Despite the noteworthy commercial interest, little is known about their supramolecular organization, especially about how such multicomponent formulations interact with cell membranes. In the present work, coarse-grained molecular dynamics simulations have been employed to study the self-assembly of a 15-component lipid nanoemulsion droplet containing vitamins A and E for skin delivery.
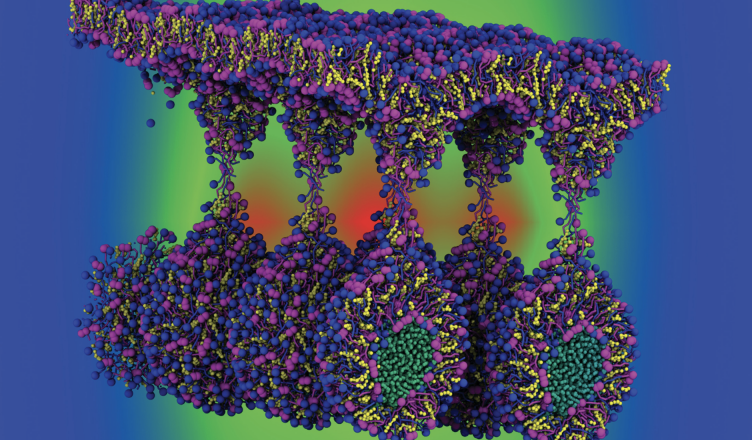
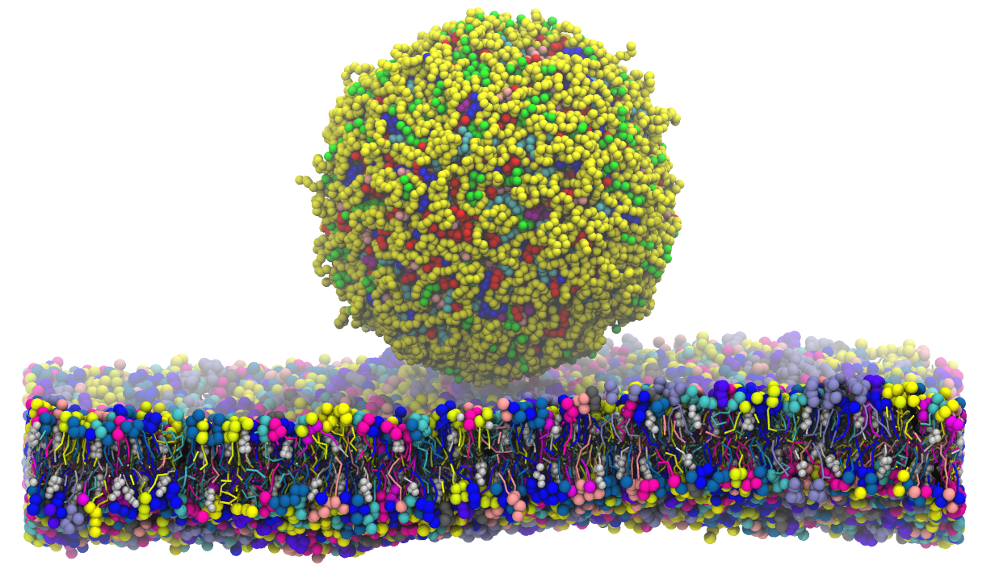 Our results display aspects of the unique “onion-like” agglomeration between the chemical constituents in the different layers of the lipid nanodroplet. Vitamin E molecules are more concentrated in the center of the droplet together with other hydrophobic constituents such as the triglycerides with long tails. On the other hand, vitamin A occupies an intermediate layer between the core and the co-emulsifier surface of the nanodroplet, together with lecithin phospholipids. Coarse-grained molecular dynamics simulations were also performed to provide insight into the first steps involved in absorption and penetration of the nanodroplet through skin membrane models, representing an intracellular (hair follicle infundibulum) and intercellular pathway (stratum corneum) through the skin. Our data provide a first view on the complex organization of commercial nanoemulsion and its interaction with skin membranes. We expect our results to open the way towards the rational design of such nanomaterials.
Our results display aspects of the unique “onion-like” agglomeration between the chemical constituents in the different layers of the lipid nanodroplet. Vitamin E molecules are more concentrated in the center of the droplet together with other hydrophobic constituents such as the triglycerides with long tails. On the other hand, vitamin A occupies an intermediate layer between the core and the co-emulsifier surface of the nanodroplet, together with lecithin phospholipids. Coarse-grained molecular dynamics simulations were also performed to provide insight into the first steps involved in absorption and penetration of the nanodroplet through skin membrane models, representing an intracellular (hair follicle infundibulum) and intercellular pathway (stratum corneum) through the skin. Our data provide a first view on the complex organization of commercial nanoemulsion and its interaction with skin membranes. We expect our results to open the way towards the rational design of such nanomaterials.
https://pubs.rsc.org/en/content/articlelanding/2022/nr/d1nr04610a
The search for more personalized drugs and therapies that minimize side effects is a very active area of research today. A much-researched approach involves developing drugs that can be absorbed through the skin, quickly accessing the bloodstream. There is a big challenge in this case: to beat the skin! It is a natural barrier that, among its various functions, works to prevent the entry of foreign compounds.
In this work using computer simulations of molecular dynamics, a skin model (> 60 thousand atoms) was built to study conditions where it would be possible to facilitate skin hydration. We observed that when applying a constant external electric field, vesicles containing water were formed, crossing the barrier. Look how interesting … water-soluble medications could already get a ride there.
Featured work was chosen as one of the covers in the magazine edition.


The control of skin permeability to specific substances (e.g., medications, vitamins, and nutrients) through the stratum corneum is a challenge. Iontophoresis is an option in spite of the lack of a detailed understanding of the underlying molecular mechanism.
In the present work, the simulations concerning the application of an external continuous electric field to stratum corneum, in a range of low intensity (0–24 mV nm-1), were carried out using the coarse-grained molecular dynamics approach.
Using a set of random seed replicas of the starting configuration, we observed that in the range of electric field intensity of 22–23 mV nm-1, water-rich lipid vesicles were formed in 20% of cases. Pores appeared in the remaining 80%. We argue that lipids undergo fast re-orientations under electric field inducing mechanical instability, which originates the pores.
We presented a simple electrostatic model to interpret the results where the mismatch between electrical permittivities of the membrane and external media and the gradient of the local electric field in the membrane surface, govern the time scales and electric fields for vesicle formation.
Our results indicate that just 10% difference between electrical permittivities of the membrane and external media decreases 1/6 the minimal time required for vesicle formation. The minimal electric field required decreases 10 times.
The control and tunning of the formation of biologically compatible vesicles, capable of transporting substances under low-intensity electric fields, has a promising application in fields such as drug therapy and dermo-cosmetics allowing the use of hydrophilic substances in dermal applications.
See all the details in https://pubs.acs.org/doi/full/10.1021/acs.nanolett.9b03881
For the first time thermoplastic polyurethane (TPU) + MXene nanocomposites are investigated by DFT. The effect of different MXene surface termination groups on TPU adsorption is investigated and the mechanisms of TPU–MXenes interactions are depicted.

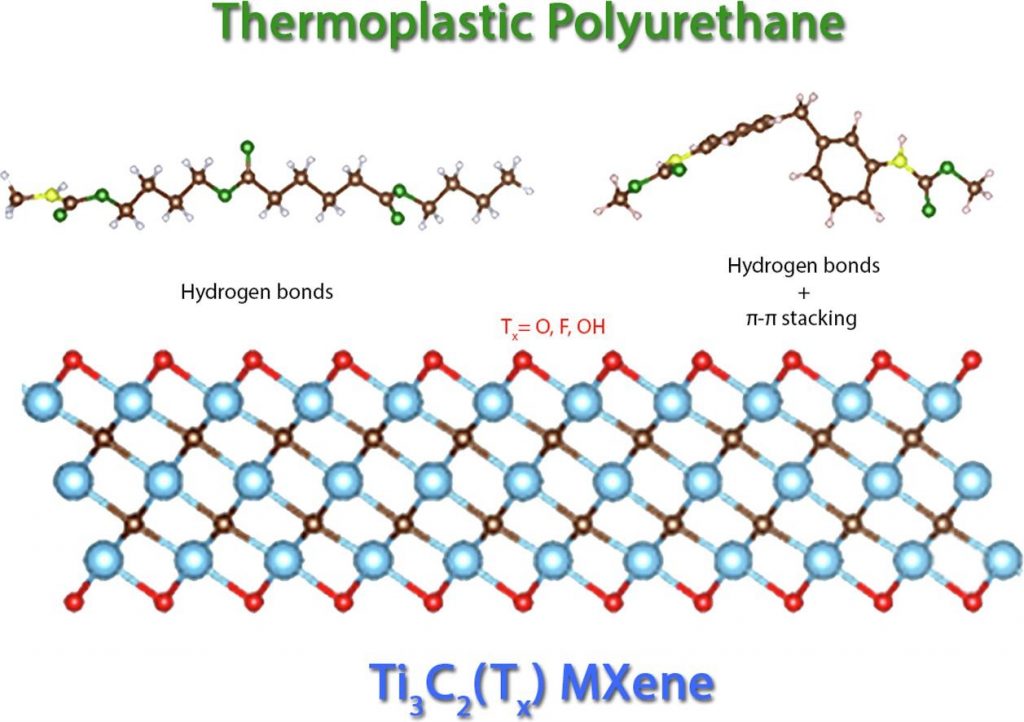
The recently discovered MXenes are promising candidates as reinforcements for nanocomposites due to their high mechanical properties, thermal and electrical conductivities. These properties are strongly affected by the presence of surface functional groups ( O,
O,  F or
F or  OH), which are related to the synthesis route employed. However, there is a lack of scientific investigations concerning the influence of such functional groups on the MXene/polymer matrix interaction. Therefore, we performed density functional theory calculations to simulate the interaction between Ti3C2 MXenes with different functional groups and thermoplastic polyurethane (TPU) based molecules. It was found that the main interaction mechanisms involved were the formation of hydrogen bonds and π-π stacking (in the aromatic ring). Moreover, while fluorine and hydroxyl terminations favored the interaction with TPU, oxygen-terminated MXene has hindered it in three of the four configurations tested. These findings indicate the relevance of controlling the MXenes surface chemistry for improving MXenes/polymer matrixes interactions in nanocomposites.
OH), which are related to the synthesis route employed. However, there is a lack of scientific investigations concerning the influence of such functional groups on the MXene/polymer matrix interaction. Therefore, we performed density functional theory calculations to simulate the interaction between Ti3C2 MXenes with different functional groups and thermoplastic polyurethane (TPU) based molecules. It was found that the main interaction mechanisms involved were the formation of hydrogen bonds and π-π stacking (in the aromatic ring). Moreover, while fluorine and hydroxyl terminations favored the interaction with TPU, oxygen-terminated MXene has hindered it in three of the four configurations tested. These findings indicate the relevance of controlling the MXenes surface chemistry for improving MXenes/polymer matrixes interactions in nanocomposites.
https://www.sciencedirect.com/science/article/pii/S0169433220312836
Advances in the synthesis and growth control at the nanoscale have allowed one to explore a variety of two-dimensional (2D) [1] materials. These systems show very unique electronic, transport, and mechanical properties [2, 3]. Of particular interest are 2D [4] topological insulators, that despite their experimental realization in HgTe/CdTe [5] quantum wells more than a decade ago, have been observed in very few systems so far [6]. Here, based on realistic material modeling at the nanoscale, we propose a new path to investigate 2D topological insulators using amorphous materials.


The topological properties of materials are, until now, associated with the features of their crystalline structure, although translational symmetry is not an explicit requirement of the topological phases. Recent studies of hopping models on random lattices have demonstrated that amorphous model systems show a nontrivial topology. Using ab initio calculations, we show that two-dimensional amorphous materials can also display topological insulator properties. More specifically, we present a realistic state-of-the-art study of the electronic and transport properties of amorphous bismuthene systems, showing that these materials are topological insulators. These systems are characterized by the topological index  2 = 1 and bulk-edge duality, and their linear conductance is quantized,
2 = 1 and bulk-edge duality, and their linear conductance is quantized,  , for Fermi energies within the topological gap. Our study opens the path to the experimental and theoretical investigation of amorphous topological insulator materials.
, for Fermi energies within the topological gap. Our study opens the path to the experimental and theoretical investigation of amorphous topological insulator materials.
See more at https://pubs.acs.org/doi/full/10.1021/acs.nanolett.9b03881 and access numerical references.
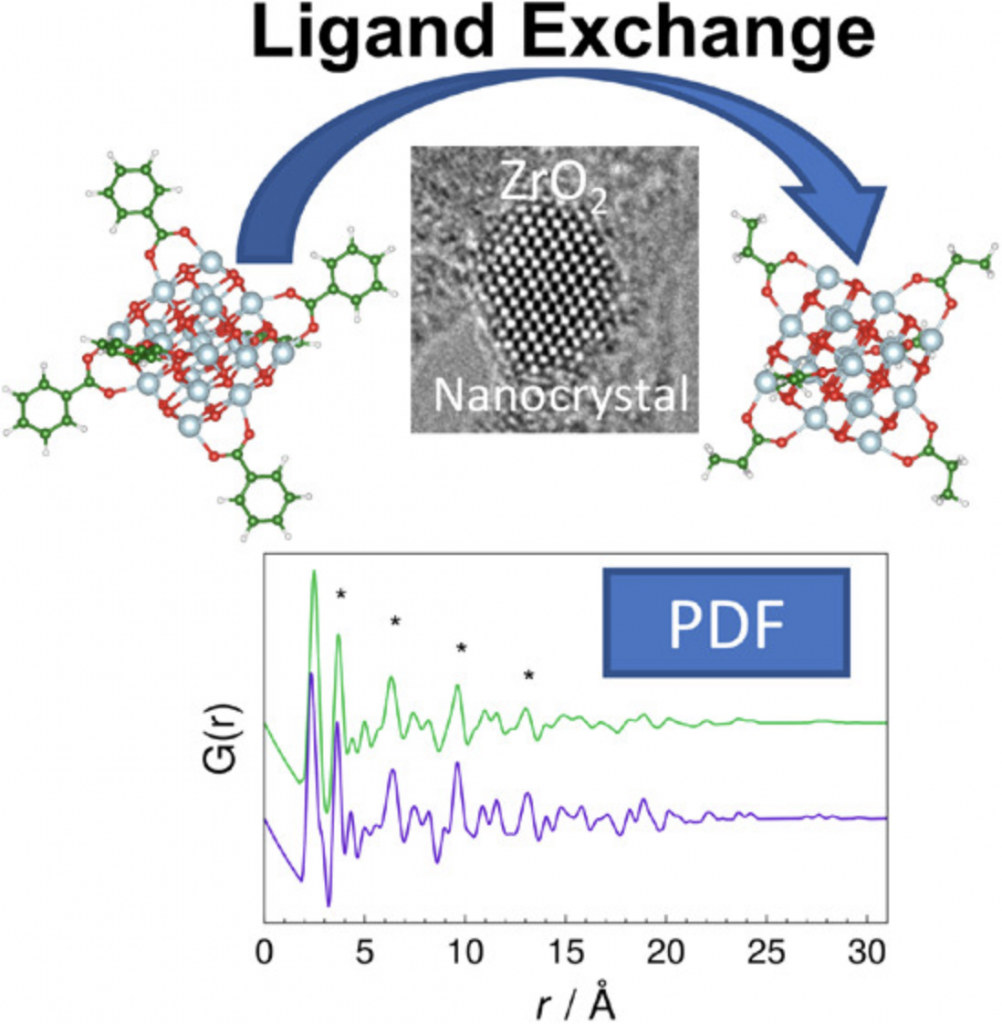 Nanocrystals (NCs) present unique physicochemical properties arising from their size and the presence of ligands. Comprehending and controlling the ligand–crystal interactions as well as the ligand exchange process is one of the central themes in NC science nowadays. However, the relationship between NC structural disorder and the ligand exchange effect in the NC atomic structure is not yet sufficiently understood.
Nanocrystals (NCs) present unique physicochemical properties arising from their size and the presence of ligands. Comprehending and controlling the ligand–crystal interactions as well as the ligand exchange process is one of the central themes in NC science nowadays. However, the relationship between NC structural disorder and the ligand exchange effect in the NC atomic structure is not yet sufficiently understood.
In this work, we combine pair distribution function analysis from electron diffraction data, extended X-ray absorption fine structure, and high-resolution transmission electron microscopy as experimental techniques and first-principles density functional theory calculations to elucidate the ligand exchange effects in the ZrO2 NC structure. We report a substantial decrease in the structural disorder for ZrO2 NCs caused by strain rearrangements during the ligand exchange process. These results can have a direct impact on the development of functional nanomaterials, especially in properties controlled by the structural disorder.
See more in https://pubs.acs.org/doi/10.1021/acs.jpclett.9b00439

See more in https://pubs.acs.org/doi/10.1021/acs.jpclett.9b00439
(DOI: https://doi-org.ez42.periodicos.capes.gov.br/10.1021/acs.jpclett.9b00439)
Trove of exotic topoloid structures has recently been predicted by searching for compounds whose calculated band structure crossing points fulfill specific symmetry requirements. Discovery of exciting physical phenomena by experimental studies of such predicted compounds is just around the corner.
 Yet, the examination of some of these assumed high-symmetry structures suggests that not always will assembly of atoms in a configuration that yields exotic topological properties be protected against energy-lowering symmetry breaking modes. Indeed, although bulk topological characteristics lead to protected surface/edge states, nothing protects bulk states from structural instability. The burden of proof for theoretical predictions of exciting physical phenomena should include some compelling hints that such phenomena can live in thermodynamically stable (or near stable) compounds. Herein, we illustrate how the use of the calculated total (electron + ion) energies of candidate structures can remove false-positive predicted topoloids from the list of likely realizable compounds, to the benefit of the much-cherished iterative process of theory-experiment materials discovery.
Yet, the examination of some of these assumed high-symmetry structures suggests that not always will assembly of atoms in a configuration that yields exotic topological properties be protected against energy-lowering symmetry breaking modes. Indeed, although bulk topological characteristics lead to protected surface/edge states, nothing protects bulk states from structural instability. The burden of proof for theoretical predictions of exciting physical phenomena should include some compelling hints that such phenomena can live in thermodynamically stable (or near stable) compounds. Herein, we illustrate how the use of the calculated total (electron + ion) energies of candidate structures can remove false-positive predicted topoloids from the list of likely realizable compounds, to the benefit of the much-cherished iterative process of theory-experiment materials discovery.
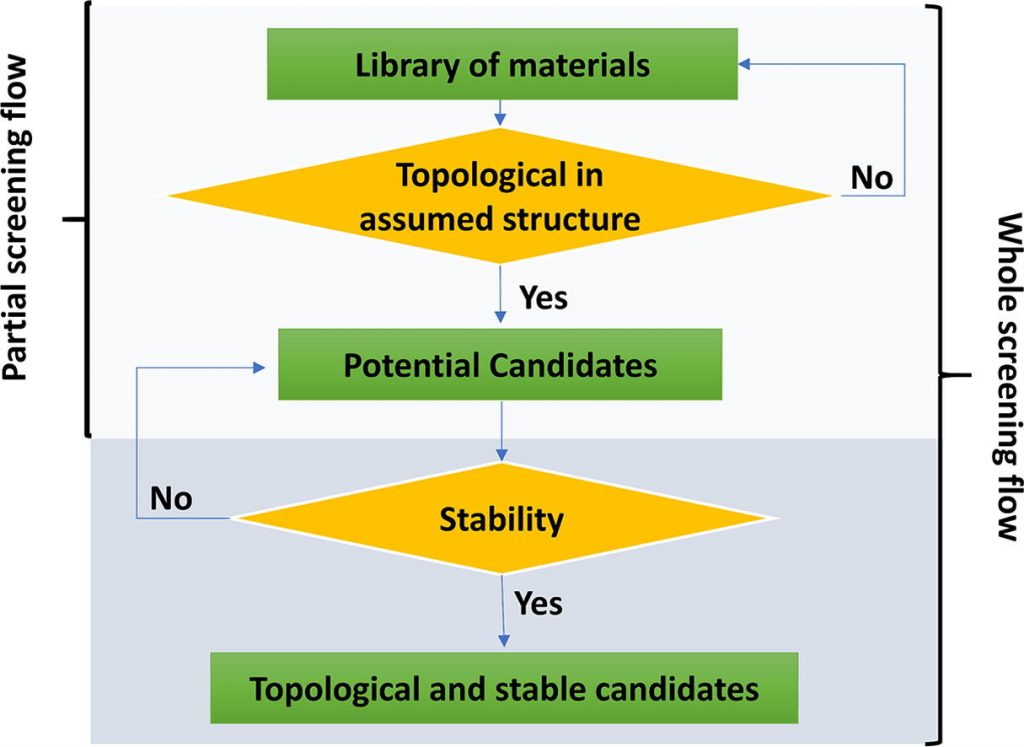
See more in https://www.sciencedirect.com/science/article/pii/S1369702119307412
Water–mineral interfaces are important for several environmental, industrial, biological, and geological processes. Gypsum, CaSO4·2H2O, is a widespread mineral of high technological, medical, and environmental relevance, but little is known about its surface structure and its interaction with water. A molecular-level understanding of gypsum/water interface is given here by a combined experimental/theoretical study.

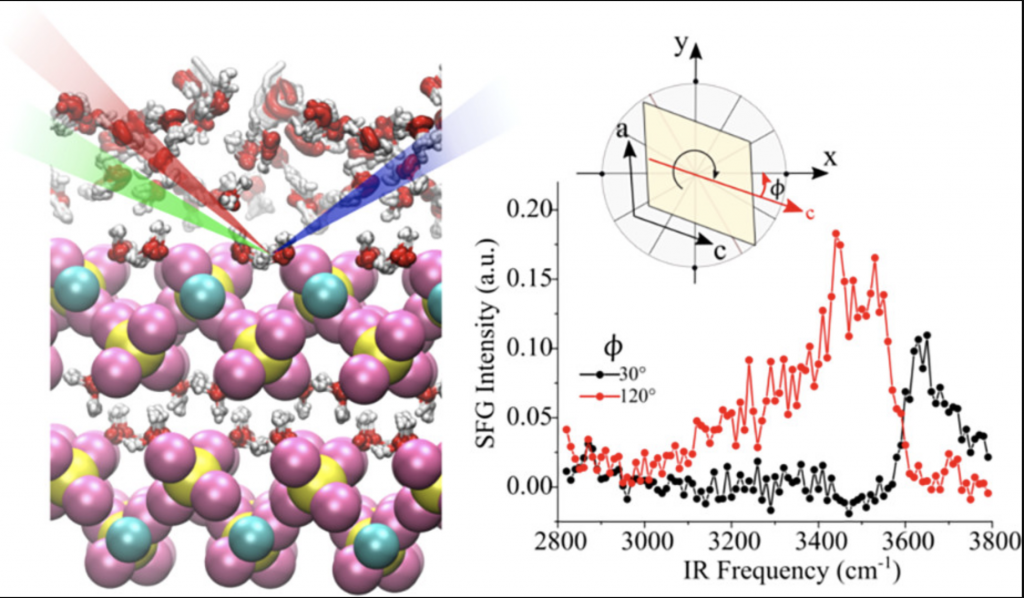
We investigate the structure and dynamics of water adsorbed from vapor on the gypsum (010) single-crystal surface at room temperature, combining sum-frequency generation (SFG) vibrational spectroscopy experiments and ab initio molecular dynamics (AIMD) simulations. The SFG spectra of gypsum at low relative humidity (RH) show an anisotropic arrangement of structural water molecules and the presence of dangling OH groups. The AIMD simulations allow a detailed assignment of the SFG spectra and show that the cleaved (010) surface rearranges to have only 25% of the OH groups pointing away from the surface. At higher RHs, the first adsorbed water layer binds to these OH groups and forms an anisotropic arrangement, but with the amount of free OH groups significantly suppressed and without any significant diffusion. Upon adsorption of a second water layer, although the topmost layer of molecules is more disordered and dynamic than the previous one, its structure is still influenced by the gypsum surface underneath because it has a much reduced amount of free OH groups with respect to the free surface of water, and a slower surface diffusion with respect to bulk water. The theoretical results corroborate the experimental ones and provide an accurate atomic characterization of the surface structure.
See more in: https://pubs.acs.org/doi/abs/10.1021/jacs.8b09907

The methodologies used to search for and develop new materials have evolved over the last decades from an Edisonian, trial and error approach toward intelligent approaches to materials discovery and design. An even more rapid change is expected over the next few years with the increasing use of artificial intelligence in many areas of chemistry and materials science. This issue of ACS Applied Materials& Interfaces features a Forum on Materials Discovery and Design, highlighting a sample of recent work in the field.

See more in: https://pubs.acs.org/doi/full/10.1021/acsami.9b10631
Defects in semiconductors can exhibit multiple charge states, which can be used for charge storage applications. Here we consider such charge storage in a series of oxygen-deficient phases of TiO2, known as Magnéli phases. These Magnéli phases (TinO2n−1) present well-defined crystalline structures, i.e., their deviation from stoichiometry is accommodated by changes in space group as opposed to point defects. We show that these phases exhibit intermediate bands with an electronic quadruple donor transitions akin to interstitial Ti defect levels in rutile TiO2. Thus, the Magnéli phases behave as if they contained a very large pseudo–defect density: ½ per formula unit TinO2n−1. Depending on the Fermi Energy the whole material will become charged. These crystals are natural charge storage materials with a storage capacity that rivals the best known supercapacitors.
As our energy requirements grow, and alternative energy sources become an integral part of most countries’ energy matrices, energy carriers, in particular charge storage systems play an ever increasing role. Li-ion batteries have played the major role in energy storage up to now, but new systems termed supercapacitors have emerged and are becoming more popular. In this case, a number of materials – mainly metal oxide thin films – provide charge storage due to the presence of defects inside its porous structure. We present an alternative strategy to design charge storage materials, based on Magneli phases of titanium oxide TinO2n−1. These can be considered as oxygen-deficient phases of TiO2, but the off-stoichiometry is accommodated by changes in the crystal structure, manifested as shear planes, as opposed to point defects, such as oxygen vacancies or Ti interstitials.
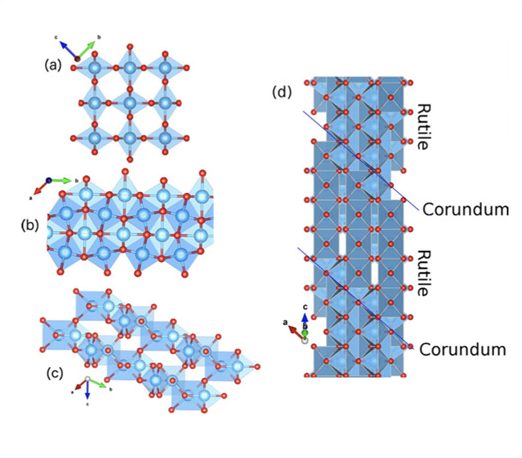
(a) Rutile TiO2, (b,c) corundum Ti2O3 view along and parallel to the c axis respectively, and (d) Magnéli phase Ti4O7 structures. Ti atoms are blue spheres enclosed by blue octahedra while oxygen atoms are red spheres on the edges of the octahedra. In (d) the blue lines enclosure the four-units rutile-like chains along the c direction, bounded by corundum-like planes restricted to the (001) planes.
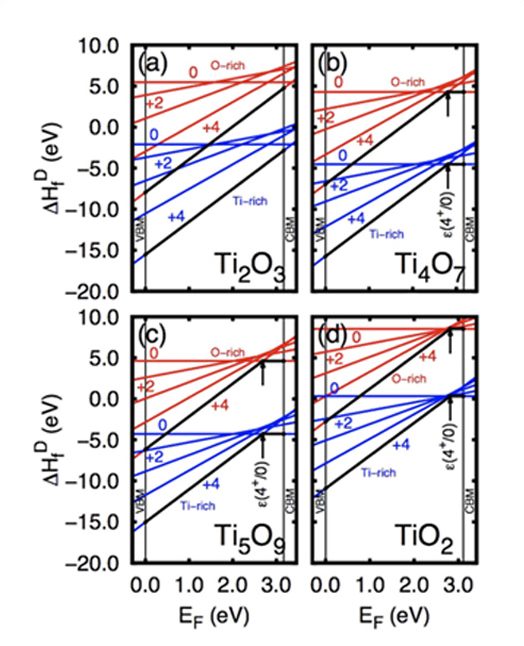
Formation enthalpies for (a) Ti2O3, (b) Ti4O7, (c) Ti5O9, (d) and Tii point defect in rutile TiO2. The Tii formation energies shown on (d) are from ref. 16. The thick black lines emphasize the lowest energy charge state for each occupation for the entire band gap span, and the transitions from +4 charge state to the neutral charge state in Ti4O7, Ti5O9, and TiO2 are also featured as ε(4+/0).
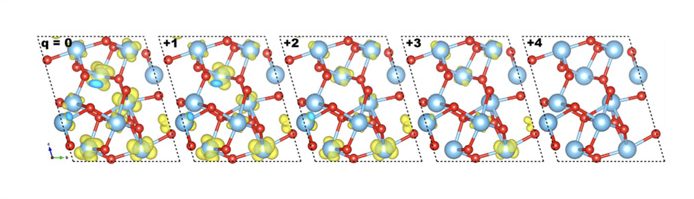
The isosurfaces are depicted for all charge states, from the neutral case to +4 from left to right. We plot the same isosurface (10−2 e · Bohr−3). The +4 charge state presents no intermediate band, the structure is presented only for the sake of completion.
See more in Charge storage in oxygen deficient phases of TiO2: defect Physics without defect
Another important work has been developed with topological insulators which was published Nature Communications. Topological insulators are a new class of matter characterized by the unique electronic properties of an insulating bulk and metallic boundaries arising from non-trivial bulk band topology. While the surfaces of topological insulators have been well studied, the interface between topological insulators and semiconductors may not only be more technologically relevant, but the interaction with non-topological states may fundamentally alter the physics. Here, we present a general model to show that this type of interaction can lead to vertical twinning of the Dirac cone, whereby the hybridized non-spin-degenerate interfacial states cross twice as they span the bulk bandgap. This hybridization leads to spin–momentum locking of non-topological states with either helical (clockwise or anticlockwise) or even anti-helical (negative winding number) spin orientation depending on the parametrization of the interaction. Model results are corroborated by first-principles calculations of the technologically relevant Bi2Se3 film van der Waals bound to a Se-treated GaAs substrate.
Topological insulators (TIs) are somewhat unique in the history of condensed matter physics, as both the nature of these materials and many of their associated exotic properties were predicted on purely theoretical grounds before experimental evidence of their existence was found. The topology of an insulator is associated with the continuous deformation of its Hamiltonian; if it can be continuously deformed to yield the band structure of another insulating system, while maintaining a bandgap throughout the deformation, then they belong to the same topological group and have the same associated Z2 topological invariant. The relatively small bandgap and large spin–orbit interaction in TIs lead to the non-trivial topology and a Z2 invariant, which is distinct from normal insulators (NIs) such as GaAs, Si or even vacuum. Although the bulk properties of TIs are similar to ordinary insulators, the interface between two materials with different topological invariants leads to the emergence of a topologically protected metallic state, which is localized to the interface and has a linear Dirac-cone-like dispersion relation, as described in the Kane–Mele model.

a) Schematic representation of the interface between a topological insulator (TI) and a normal insulator (NI), z is normal to the interface. (b) The band structures of the semiconductor (shown in red) and topological insulator (shown in blue) are depicted for the case of type-II alignment, whereby the VBM of the semiconductor lies within the bulk gap of the topological insulator. The Δ parameter in the Hamiltonian model is the VBM energy relative to the Dirac point. (c) Band structure at the interface in the absence of mutual interaction between the TI and NI. The topological interface state is shown in blue with linear dispersion and the semiconductor-derived bands are shown in red with parabolic dispersion. The degeneracy of the bands are labelled, either (1) non-degenerate or (2) doubly degenerate, and the black dots indicate points that are required to be doubly degenerate due to the preservation of TRS. The dashed box indicates the region in which the NI state and the TI state cross. (d) The effect to c when interaction is turned on. The effect of the interaction is highlighted in the dashed box, in which the interaction leads to an anticrossing between the previously doubly degenerate NI state and the singly degenerate TI state, which requires the interconversion of the character of semiconducting bands and TI bands. As a result, neither of the double degeneracies at Γa can cleanly be labelled as the Dirac point, as both consist of the crossings of state that change from TI to semiconductor character.
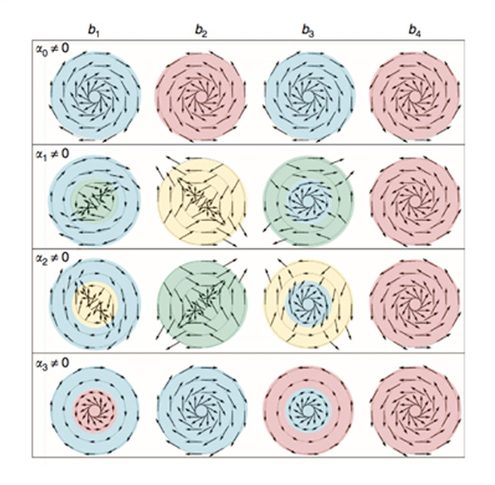
Each figure shows the spin orientation for a particular band for various concentric circles in the kx–ky plane, with the centre being the Γ-point. They are arranged in columns of differing band number, labelled (b1–4) in increasing energy. Each row corresponds to considering a different type of interaction for Vint. In each case, we assume that Vint is parameterized by a single parameter and that all of the other parameters vanish. The choice for non-vanishing parameter, αi≠0, is indicated for each row. The blue- and red-shaded regions indicate left- and right-handed spin texture, respectively. The yellow and green regions indicated left- and right-handed anti-helical spin texture, where the spin has a negative winding number.
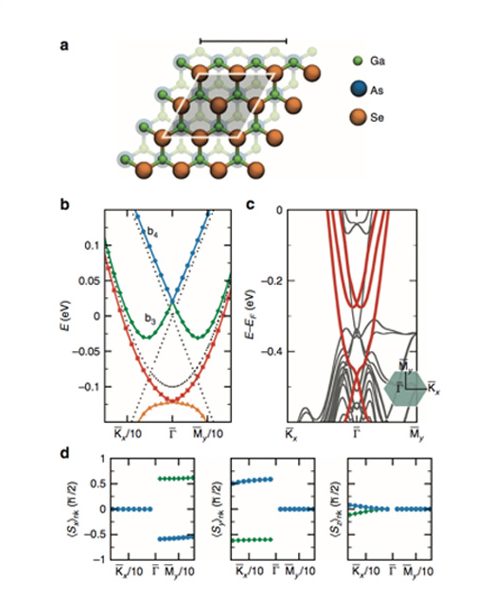
(a) Top view of a ball-and-stick model for GaAs(111) surface with 0.75 ML of Se treatment. The unit cell is shaded in grey; scale bar, 5 Å. The stacking sites of the first atomic layer of Bi2Se3 are labelled by H3, T4 and T1. (b) Chemical stability map for the GaAs(111) surface. The shaded regions indicate which Se surface coverage of the GaAs(111) surface is the most stable as a function of the chemical potentials of As and Se, μAs and μSe. (c) Side view of a ball-and-stick model for Bi2Se3/GaAs interface with 0.75 ML of Se treatment and H3 stacking. The shaded area shows the interface region; scale bar, 1 nm. (d) Electronic band structure for Bi2Se3/GaAs with 0.75 ML of Se treatment. Four bands near the Fermi level are highlighted in red for comparison with the effective Hamiltonian.